DSP 與剩餘定理

DSP (Digital Signal Processing) 真的很難很難，我已經上過數不清的這方面的課了，好像仍然只是一知半解，一堆難以理解的理論、算法，本來好像有些懂了，尤其是基礎的部分，然而看得愈多就覺得愈像天書，真是難以理解這些大教授們是怎麼發展出這些理論的。

更可怕的是，這些有名理論與算法，許多都是數百年前就已經找到，比較現代的理論與算法，也至少有 30 ~ 40 年以上的歷史，直到近代才被廣泛的應用在各種領域上。

例如發源自古中國的「剩餘定理」，竟然跟應用周期性傅立葉轉換 (Periodic Fourier Transform) 的快速迴旋算法 (Fast convolution)，有著道不清說不明連我也快要搞不懂的關係。

呵啊，剩餘定理真的很令人懷念啊，記得小學的時候，被強迫要做很多的算術練習，其中就有這個一題，完全是抄自古人的題目。

一個整數，除以 3 餘 2，除以 5 餘 3 ，除以 7 餘 2，求這個整數？

在 1700 多年前孫子算經原著中是這麼寫的：

有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？

利用有點複雜的公倍數算法可以解出 233 這個答案。

然後，經過數十百年的推演，就變成了 x=x₀+n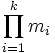 （對所有問題的公解）
（參考來源：wikipedia）

啊啊啊，什麼跟什麼啊，現在你懂了吧，就是這樣，看懂一個算法常常就要花去我半個多小時，完成一個練習更要花去更多時間，有時還不一定能完全理解，真是令人喪氣。

不過有時順利的解開問題，就好像變魔術一樣，有一種令人驚喜的欣然快感，只是那過程實在是讓人不想再經歷一遍。

跟這些天書文字們還有整個學期的戰鬥呢，唉，希望後天的考試不會出現太誇張的難題啊！